For best experience please turn on javascript and use a modern browser!
You are using a browser that is no longer supported by Microsoft. Please upgrade your browser. The site may not present itself correctly if you continue browsing.
uva.nl
Institute for Advanced Study (IAS) null

3.5 Dynamic importance of network nodes is poorly predicted by static structural features

Casper van Elteren, Rick Quax and Peter Sloot

Keywords: Complex systems; Driver node identification; Information theory; Network science 

Authors on the article: 

One of the most central questions in network science is: which nodes are most important? Often this question is answered using structural properties such as high connectedness or centrality in the network. However, static structural connectedness does not necessarily translate to dynamical importance. To demonstrate this, we simulate the kinetic Ising spin model on generated networks and one real-world weighted network. The dynamic impact of nodes is assessed by causally intervening on node state probabilities and measuring the effect on the systemic dynamics. The results show that structural features such as network centrality or connectedness are actually poor predictors of the dynamical impact of a node on the rest of the network. A solution is offered in the form of an information theoretical measure named integrated mutual information. The metric is able to accurately predict the dynamically most important node (‘driver’ node) in networks based on observational data of non-intervened dynamics. We conclude that the driver node(s) in networks are not necessarily the most well-connected or central nodes. Indeed, the common assumption of network structural features being proportional to dynamical importance is false. Consequently, great care should be taken when deriving dynamical importance from network data alone. These results highlight the need for novel inference methods that take both structure and dynamics into account.

We believe the results would be valuable for members of the IAS community as the different themes housed at the IAS are involved with network thinking, applying network science directly, using causal loop diagrams, and or performing agent-based simulations. Understanding how (for example) resilience occurs in health science, criminal systems, or how segregation occurs in school is fundamentally grounded in how the structure of the system interacts with its effective output (the dynamics) [9–11]. It therefore touches on fundamental themes that are running at the IAS ranging from dynamical social systems, coupled human social systems to health science complexity and foundational methods for understanding complex systems. We would like to contribute in the goal of the IAS to push the boundary on understanding emergent behavior in complex systems.

References

1. Epskamp, S., Borsboom, D. & Fried, E. I. Estimating Psychological Networks and Their Accuracy: A Tutorial Paper. Behavior Research Methods 50,195–212.issn:1554-3528(Feb. 2018).
2. Duijn, P. A. C. Detecting and Disrupting Criminal Networks: A Data Driven Approach isbn: 978-90-77595-41-1 (2016).
3. Duijn, P. A., Kashirin, V. & Sloot, P. M. The Relative Ineffectiveness of Criminal Network Disruption. Scientific Reports 4. issn: 20452322 (2014). 4. Luke, D. A. & Stamatakis, K. A. Systems Science Methods in Public Health: Dynamics, Networks, and Agents. Annual Review of Public Health 33, 357–376. issn: 0163-7525, 1545-2093 (Apr. 2012).
5. Jayaweera, I. M. L. N., Perera, K. K. K. R. & Munasinghe, J. Centrality Measures to Identify Traffic Congestion on Road Networks : A Case Study of Sri Lanka. 13, 13–19 (2017).
6. Borgatti, S. P. Centrality and Network Flow. Social Networks 27, 55–71. issn: 03788733 (2005).
7. Borgatti, S. P. & Everett, M. G. A Graphtheoretic Perspective on Centrality. Social Networks 28, 466–484. issn: 03788733 (2006).
8. van Elteren, C., Quax, R. & Sloot, P. Dynamic Importance of Network Nodes Is Poorly Predicted by Static Structural Features. Physica A: Statistical Mechanics and its Applications, 126889. issn: 03784371 (Jan. 2022).
9. Harush, U. & Barzel, B. Dynamic Patterns of Information Flow in Complex Networks. NatureCommunications8,1–11.issn: 20411723 (2017).
10. Gao, J., Barzel, B. & Barabási, A.-L. Universal Resilience Patterns in Complex Networks. Nature 536, 238–238. issn: 00280836 (2016).
11. Barzel, B. & Barabási, A.-L. Universality in Network Dynamics. Nature Physics 9, 673681. issn: 1745-2473 (2013). 

Figure 1: What node is most important? Various centrality features can be used to infer the structural most important. In this paper we test out how predictive centrality features are on synthetic and real-world networks. The inferred driver node is indicated by a dotted black line above. By simulating dynamics on graphs, causal driver nodes are inferred through nudge interventions. The results show that centrality metrics are generally not predictive for unperturbed system dynamics (low causal intervention; compare bottom left and right 4 subplots). A solution is offered by means of information theory with a novel measure dubbed integrated mutual information.
Figure 2: Extended results for real-world network. (A) Information impact is trends linearly for causal impact for nodes for medium to high noise in low causal interventions. This implies that the inferred driver node through integrated mutual information is predictive for determining the driver node for unperturbed system dynamics. Forhighcausalintervention this effect disappears as the system dynamicsdivergefromits“natural” trajectories. (B) Inferred driver node for medium noise for various centrality metrics (top), integrated mutual information (middle), and causal interventions (bottom). (C) Statistical quantification of driver node identification using Jaccard indices. See https://doi.org/10.1016/j.physa.2022.126889 for extended analysis on synthetic and real-world networks.
Read the full article here

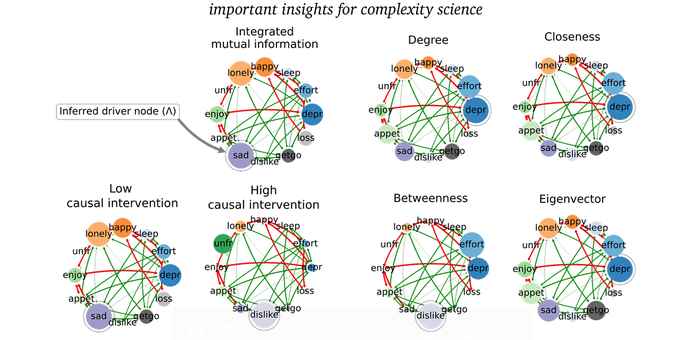
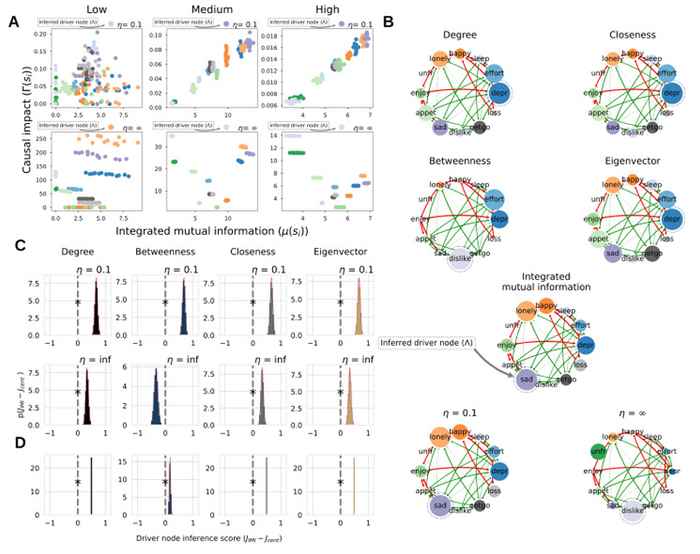
Elteren, C. van, Quax, R., Sloot, P. (2022) Dynamic importance of network nodes is poorly predicted by static structural features. Physica A: Statistical Mechanics and its Applications, Volume 593. https://doi.org/10.1016/j.physa.2022.126889.