Author Peter Bolhuis on the article: 

Natural systems can comprise an intricate and complex web of interacting constituents, giving rise to interesting and unexpected emergent phenomena. An obvious example is molecular biology, but one can also think of self-organizing matter, or auto-catalytic chemical reaction networks. When studying complex biomolecules such as proteins or DNA, a first step often consists in the determination of their structures, for example, using X-ray crystallography or cryo-electron microscopy. By revealing a wide range of structure-function relationships, this approach has enabled major advances in molecular biology in the last 50 years.  Such experiments are often combined with computational methods, which yield the motions of all the atoms in a molecular system as dictated by thermal fluctuations, resolving atomistic structures that are otherwise elusive in experiments. However, the use of approximated atomic interactions yields results that are not entirely accurate.  To improve structural models, molecular dynamics simulations are often combined with experimental data.  Statistical methods developed in the last decade are now able to increase the accuracy of molecular dynamics simulations by incorporating experimental information, and allow the determination of thermodynamic ensembles of structures (see for a perspective doi.org/10.1016/j.sbi.2018.10.006 ). However, one would like to go even further, by obtaining ‘kinetic ensembles’, comprising the structures of the different states of a molecular system, their populations and their interconversion rates.  The latter are even harder to predict correctly. One long-standing idea was to make use of knowledge about experimental rates, but up to now it was still unclear how to include these into the simulations.

In our paper we introduce a method of imposing known rate constants as constraints in molecular dynamics simulations, based on a combination of the maximum-entropy (MaxEnt) and maximum-caliber principles (MaxCal). Originating from information theory, the MaxEnt and MaxCal principles are powerful concepts in statistical physics and yield optimal models given imposed constraints. Starting from an existing ensemble of dynamical trajectories (a.k.a paths), the novel method reweights each path in order to match the calculated and experimental interconversion rates of a molecular transition of interest, while minimally perturbing the prior path distribution. This kinetically corrected ensemble of trajectories leads to improved structure, kinetics and thermodynamics, as well mechanistic insights that may not be readily evident directly from the experiments.

We illustrate the application of the method to model systems, including all atom molecular simulations of protein folding. Our results show that by combining experimental rate constants and molecular dynamics simulations this approach enables the determination of transition states, reaction mechanisms and free energies. We anticipate that this method will extend the applicability of molecular simulations to kinetic studies in structural biology, and that it will assist the development of force fields to reproduce kinetic and thermodynamic observables.  As the outcomes of molecular processes often depend on the rates at which they occur, with this new method we can improve our ability to determine molecular mechanisms responsible for biomolecular function and dysfunction.  

The approach is generally applicable to a wide range of systems in biology, physics, chemistry, and material science, and possibly even applicable to any process where the interaction of many constituents gives rise to ‘kinetic ensembles’. As such, it opens up many possibilities for improving our understanding of nature at the microscopic scales.

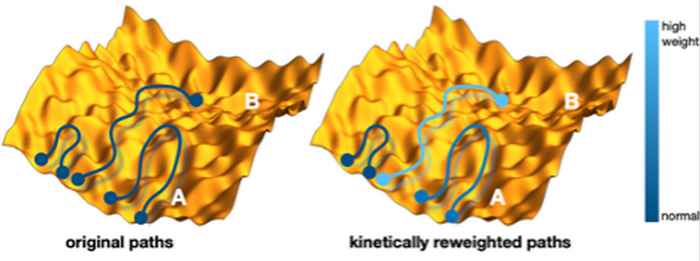
Figure: schematic illustration of the reweighting of the molecular dynamics trajectories. Each trajectory is a curve in a high dimensional energy landscape, here represented as a yellow rough hilly surface. Each point on the path represent a structure at a certain time. Paths start and end in one of the blue circles.  Left are the originals paths starting at an initial structure A, where only a few paths make It over the rough energy barrier to another structure B. Right is the kinetically reweighted path ensemble, where the color indicates the strength of the path weight. These weights are at the heart of the new method.

Brotzakis, Z. F., Vendruscolo, M., & Bolhuis, P. G. (2021). A method of incorporating rate constants as kinetic constraints in molecular dynamics simulations. Proceedings of the National Academy of Sciences, 118(2), e2012423118.